Impulse approximation

ある空間を運動している質点が重力ポテンシャルの影響を受けて運動の方向を変える散乱過程を考えます. ここでは簡単のため, 以下のような状況を考えます.

重力ポテンシャルは不変とします. 重力を及ぼす物体は運動している質点に比べて重たいので, 重力源の運動は考えなくて良いという状況に相当します.
重力ポテンシャルは中心からの距離 \(r\) のみの関数として表現できるとします.

座標系の原点を重力ポテンシャルの中心にとります. 質点の位置を \(\mathbf{r}\) で表現します. また, 中心からの距離 \(r (= |\mathbf{r}|)\) に含まれる質量を \(M(r)\) で表すと, 質点が受ける力の大きさは以下の式でかけます.

\[ \mathbf{F}(\mathbf{r}) = -G \frac{M(r) \, m}{r^2} \frac{\mathbf{r}}{r}. \]

無限遠から出発した質点が等速直線運動をすると思って軌跡を外挿すると, ある直線 \(l_0\) になります. この直線と重力ポテンシャルの中心までの距離が最小になる地点を \(\mathbf{b}\) で表します. このベクトルの大きさ \(b (=|\mathbf{b}|)\) を衝突パラメタと呼びます. ここで考えている過程は, 質点の初期速度 \(v\) と衝突パラメタ \(b\) を与えることで一意に決めることができます.

質点の運動は重力の影響をうけて時々刻々と変化します. この運動は運動方程式を積分することで求めることができます. しかし, 運動の変化がそれほど大きくない場合には, 質点が受ける力積は無限遠から等速直線運動をする仮想的な質点が受ける力積と大差ありません. 重力ポテンシャルを通過した前後の運動状態の変化しか興味がなければ, 時々刻々の運動の変化を考慮せずに力積を計算して, 散乱後の速度を求めるという近似が成り立ちます. 本来は運動量は有限の時間をかけて連続的に変化しますが, 計算した力積 (impulse) から運動量の変化を見積もるため, この手法はインパルス近似 (impulse approximation) と呼ばれます.

移動する質点の位置を \(\mathbf{r}(t) = (vt, b)\) で表すと力積は以下のように計算できます.

\[ \mathbf{I} = \int^{+\infty}_{-\infty} \mathbf{F}(t) \mathrm{d}t = -Gm \int^{+\infty}_{-\infty} M(r)\frac{\mathbf{r}}{r^3} \mathrm{d}t. \]

ただし \(r = \sqrt{(vt)^2 + b^2}\) です. また, 被積分関数の対称性から力積 \(\mathbf{I}\) の \(x\) 方向成分は 0 になります. よって \(y\) 方向成分だけを考慮すれば十分です. \(\xi = vt\) とおいて整理すると以下の式を得ます.

\[ {I_y} = -\frac{Gmb}{v} \int^{+\infty}_{-\infty} \frac{M(\sqrt{\xi^2 + b^2})}{\bigl({\xi^2 + b^2}\bigr)^{3/2}} \mathrm{d}\xi. \]

質点がもともと持っていた運動量は \(\mathbf{P} = (mv, 0)\) でした. ポテンシャルを通過することによっ見積もった分だけ \(y\) 方向の運動量が変化すると近似できます.

\[ (mv, 0) \to (mv, I_y). \]

しかし, 一般に重力ポテンシャルは無限遠 (\(r \to \infty\)) で 0 になります. 通過前と通過後で比較したときに無限遠では運動エネルギーが一致していなければいけません. インパルス近似での運動エネルギーの変化は以下のとおりです.

\[ \frac{1}{2}mv^2 \to \frac{1}{2}mv^2 \left(1 + \left(\frac{I_y}{mv}\right)^2\right) \]

インパルス近似がよい近似を与えるためには \(|I_y| \ll |mv|\) が求められます.

Point-mass potential

質点がつくる重力ポテンシャルでは \(M(r)\) は距離 \(r\) に依存しない定数 \((M)\) になります. よって力積は以下のように計算できます.

\[ {I_y} = -\frac{GMmb}{v} \int^{+\infty}_{-\infty} \frac{1}{\bigl(\xi^2 + b^2\bigr)^{3/2}} \mathrm{d}\xi = -\frac{GMmb}{v} \frac{2}{b^2} = -\frac{2GMm}{vb}. \]

\(I_y \propto v^{-1}b^{-1}\) となります. 無限遠での速度 \(v\) が小さいほど質点の通過時間は長くなり, 力積は通過時間に比例して大きくなります. また衝突パラメタが小さいと受ける力が大きくなるので力積も大きくなります.¹

質点がもともと持っていた運動量 \(mv\) との比は以下のとおりです. 整理すると初期の運動エネルギーと最接近点での重力ポテンシャルとの比になります.

\[ \frac{I_y}{mv} = -\frac{2GM}{v^2b} = - \left. G\frac{Mm}{b} \middle/ \frac{1}{2}mv^2 \right. \]

衝突パラメタが \(b + \mathrm{d}b\) のケースを考えます. \(\mathrm{d}b\) を微少量と考えると, 力積 \(I_y\) の変化量 \({\mathrm{d}}I_y\) は以下のようにかけます.

\[ {\mathrm{d}I_y} = \frac{2GMm}{vb^2} {\mathrm{d}b} \]

無限遠から \(\mathrm{d}b\) の距離で並走してきた 2 つの質点 (互いの重力は無視できるとする) を考えます. 2 つの質点とともに移動する系から見ると, この力積は質点を引き剥がすように働きます (潮汐力). この力積 (速度変化) が 2 つの質点を束縛している力よりも大きい場合には系が破壊されます. 2 つの質点が同じ質量 \(m\) を持つと仮定して大雑把に見積もってみます. 力積による相対速度変化の大きさは以下のように計算できます.

\[ \delta{v_r} = \frac{{\mathrm{d}}I_y}{m} = \frac{2GM}{vb^2}\Delta \]

ただし, 視認性のために \(\Delta = {\mathrm{d}}b\) としました. 参考までにこの速度変化に対応する運動エネルギーと重力ポテンシャルの和がゼロになる条件を考えます.

\[ \frac{1}{2}m (\delta{v_r})^2 - G\frac{m^2}{\Delta} = 0, \quad \Delta = \left(\frac{v^2 b^4 m}{2 G M^2}\right)^{1 \over 3} \]

散乱体の質量 \(M\) が大きいほど, 衝突パラメタ \(b\) が小さいほど, また, 遭遇速度 \(v\) が小さいほど, より近接した質点を引きはがせます.

Uniform density sphere

空間密度 \(\rho\) が一様なポテンシャルによる散乱を考えてみます. ただし, 無限遠まで広げてしまうと無限大の質量が必要になるため, ここでは重力源は中心から半径 \(R\) の球内にのみ存在するとします.

\[ M(r) = \begin{cases} \displaystyle \frac{4\pi}{3}R^3 \rho & r \ge R \\ \displaystyle \frac{4\pi}{3}r^3 \rho & r < R \end{cases} \]

力積の積分は球の中にいるケースと外にいるケースで分けて計算します. まずは球の外にいるケースを計算します.

\[ \begin{aligned} (I_y)_\text{out} & = -\frac{4\pi}{3} \frac{G R^3 \rho mb}{v} \left[ \int^{-\sqrt{R^2-b^2}}_{-\infty} \frac{1}{\bigl(\xi^2 + b^2\bigr)^{3/2}} \mathrm{d}\xi + \int^{+\infty}_{+\sqrt{R^2-b^2}} \frac{1}{\bigl(\xi^2 + b^2\bigr)^{3/2}} \mathrm{d}\xi \right] \\ & = - \frac{8\pi}{3} \frac{G R^3 \rho mb}{v} \left. \frac{\xi}{b^2\sqrt{\xi^2 + b^2}} \right|^{\infty}_{+\sqrt{R^2 - b^2}} \\ & = - \frac{8\pi}{3} \frac{G R^3 \rho m}{v}\frac{1}{b} \left( 1 - \sqrt{1 - \frac{b^2}{R^2}} \right) \end{aligned} \]

次に球の中にいるケースを計算します.

\[ (I_y)_\text{in} = -\frac{4\pi}{3} \frac{G \rho mb}{v} \int^{+\sqrt{R^2-b^2}}_{-\sqrt{R^2-b^2}} \mathrm{d}\xi = - \frac{8\pi}{3} \frac{G R^3 \rho m}{v} \frac{b}{R^2} \sqrt{1 - \frac{b^2}{R^2}} \]

合計すると力積は以下のように整理できます.

\[ \begin{aligned} I_y & = (I_y)_\text{out} + (I_y)_\text{in} \\ & = - \frac{8\pi}{3} \frac{G R^3 \rho m}{v} \left[ \frac{1}{b} \left( 1 - \sqrt{1 - \frac{b^2}{R^2}} \right) + \frac{b}{R^2} \sqrt{1 - \frac{b^2}{R^2}} \right] \\ & = - \frac{8\pi}{3} \frac{G R^3 \rho m}{v} \frac{1}{b} \left[ 1 - \left(1 - \frac{b^2}{R^2}\right)^{\frac{3}{2}} \right] \end{aligned} \]

散乱体の総質量 \(M = 4\pi \rho R^3/3\) をつかって式を整理します. 括弧の中の第一項は点源のケースに対応しています. 重力源が広がっている効果は主に第二項が表現しています. この項は \(b=R\) でゼロになるので, 質点ポテンシャルによる解と連続的につながっていることがわかります.

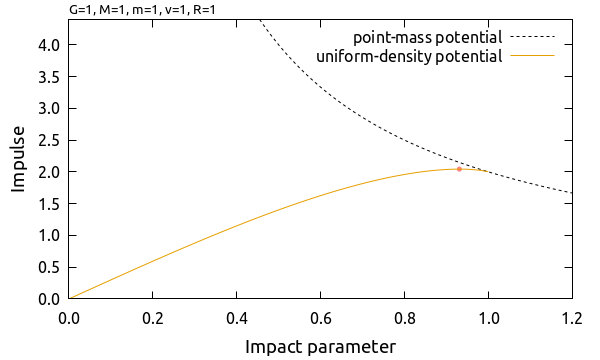
\[ I_y = - \frac{2 G M m}{v} \frac{1}{b} \left[ 1 - \left(1 - \frac{b^2}{R^2}\right)^{\frac{3}{2}} \right] \]

以下に質点が作る重力ポテンシャルと密度一定球が作る重力ポテンシャルの力積 \(I_y\) の絶対値を衝突パラメタ \(b\) の関数として表示しました. \(b = R\) となる点で連続的につながっていることがわかります.

先ほどと同様に衝突パラメタが \(b + \mathrm{d}b\) となったときの力積の変化量 \(\mathrm{d}{I_y}\) を考えます.

\[ \begin{aligned} {\mathrm{d}{I_y}} & = \frac{2GMm}{v} \left[ \frac{1}{b^2} \left(1 - \sqrt{1 - \frac{b^2}{R^2}}\right) - \frac{2}{R^2} \sqrt{1 - \frac{b^2}{R^2}} \right] {\mathrm{d}b} \\ & = \frac{2GMm}{v} \frac{1}{b^2} \left[ 1 - \left(1 + 2\frac{b^2}{R^2}\right) \sqrt{1 - \frac{b^2}{R^2}} \right] {\mathrm{d}b} \end{aligned} \]

\({\mathrm{d}{I_y}}\) は \({b} = (3/4)^{1/4}R\) で 0 になり, 力積 \(I_y\) はこの点 (上記グラフの赤丸の位置) で極値をとります. また \(b=R\) を代入すると質点が作るポテンシャルの式と一致するため, 両者は \(b = R\) でなめらかに接続することがわかります.

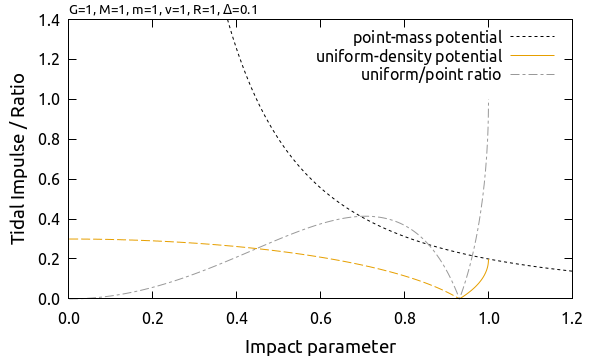
下の式の第一項は質点が作るポテンシャルに依る潮汐力に対応することがわかります. 重力源が広がっている効果は第二項にあらわれており, 潮汐力を打ち消す効果を示すことが期待できます. 潮汐効果の大きさをグラフに図示しました. 破線で示した領域では潮汐効果の向きが質点がつくるポテンシャルの場合と逆向きになっていることに注意してください.

潮汐効果の大きさは質点が作るポテンシャルに比べて小さく, \(b/R < (3/4)^{1/4}\) の領域では最大で 41% 程度に留まることがわかります. 重力源が広がっているケースではポテンシャルの勾配の変化が緩やかになっているため, 潮汐力として働きにくくなっていると解釈できます.

Tidal impulses against impact parameters

Polytrope-like potential

To be updated…

空間密度が中心からの距離に応じてなだらかに減少するケースを考えてみます. ここでは \(n > 0\) として以下の関係式をで空間密度を与えます.

\[ \rho(r) = \rho_0 \left(1 + \left(\frac{r}{r_c}\right)^2 \right)^{-n/2} \]

\(\rho_0\) は中心での密度, \(r_c\) は典型的な大きさを表します. この形式の密度分布はいくつかの物理モデルで現れる密度分布を表現できます. 例えば \(n=5\) の密度分布はポリトロープ指数が \(5\) の静水圧平衡を仮定した密度分布と一致します. また, 等温ガス球の密度分布は \(\rho(r) \propto r^{-2}\) なので \(n=2\) の密度分布は良い近似を与えます. この章では (不正確ですが) 暫定的にこの質量分布が作るポテンシャルを Polytrope-like と表現します.

\(M(r)\) は以下の式で計算できます.

\[ M(r) = \int^{r}_0 4\pi r'^2 \rho(r') \mathrm{d}r' = 4\pi\rho_0 \int^{r}_0 \frac{r'^2}{(1 + (r'/r_c))^{n/2}} \mathrm{d}r' \]

この積分は超幾何関数 \(_2F_1(\cdot,\cdot;\cdot;x)\) で記述できます (要確認).

\[ M(r) = \frac{4\pi}{3}\rho_0 r_c^3 \int^{r/r_c}_{0} \frac{\xi^2}{(1+\xi^2)^{n/2}} {\mathrm{d}\xi} = \frac{4\pi}{3}\rho_0 \, r_c^3 \left(\frac{r}{r_c}\right)^3 {_2F_1}\left( \frac{3}{2}, \frac{n}{2}; \frac{5}{2}; -\frac{r^2}{r_c^2} \right) \]

この関数が \(r \to \infty\) で発散しないためには \(n > 3\) でなければなりません. \(n = 4, 5, 6, 7\) のときはそれぞれ以下の値に収束します.

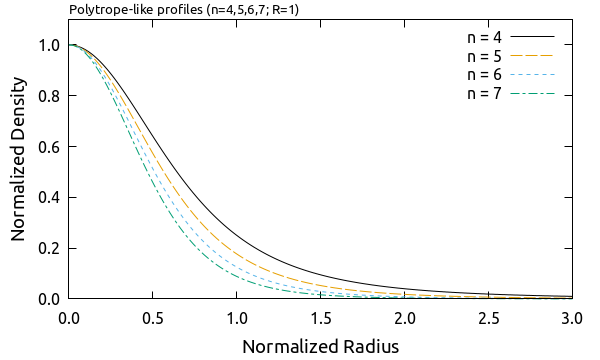
\[ M(r) \to \left\{ \pi^2 \rho_0 r_c^3,~ \frac{4\pi}{3}\rho_0 r_c^3,~ \frac{\pi^2}{4}\rho_0 r_c^3,~ \frac{8\pi}{15}\rho_0 r_c^3 \right\} \]

それぞれの密度分布を半径の関数として表示すると以下のようになります.

力積の計算式は以下のようになります.

\[ I_y = -\frac{4\pi}{3} \frac{G \rho_0 mb}{v} \int^{+\infty}_{-\infty} {_2F_1}\left( \frac{3}{2}, \frac{n}{2}; \frac{5}{2}; -\frac{\xi^2 + b^2}{r_c^2} \right) \mathrm{d}\xi \]

(少なくとも) \(n = 5, 7\) のときは解析解があります.²

\[ \begin{aligned} I_y & = - \frac{4\pi}{3} \frac{G \rho_0 mb}{v} \times \left\{ \frac{2 r_c^3}{b^2 + r_c^2}, \frac{4 r_c^3 (b^2 + 2 r_c^2)}{5 (b^2 + r_c^2)^2} \right\} \\ & = - \frac{2 G M m}{v}\frac{1}{b} \times \left\{ \frac{b^2}{b^2 + r_c^2}, \frac{b^2(b^2 + 2 r_c^2)}{(b^2 + r_c^2)^2} \right\} \end{aligned} \]

括弧の前の項は質点が作るポテンシャルに依る力積に対応します. 質量分布が広がっている効果は括弧の中の項で表されます. \(n=5, 7\) のどちらのケースでも括弧の中の項は 1 を超えません. また, \(b \to \infty\) で 1 に収束するため, インパクトパラメタが大きい極限では質点が作るポテンシャルによる力積と一致します.

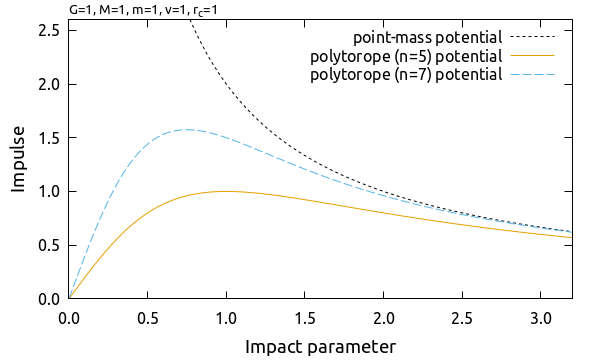
以下に力積とインパクトパラメタの関係を図示します. 特徴的な半径 \(r = r_c\) 付近でピークを持ち, 外側では質点が作るポテンシャルに依る力積に漸近します.

Impulse of the polytrope-like potentials

\(n=5, 7\) のケースについて衝突パラメタが \(b + {\mathrm{d}}b\) となったときの力積の変化 \(\mathrm{d}I_y\) を計算します. 括弧の前の項は質点が作るポテンシャルによる潮汐効果に対応しています.

\[ \begin{aligned} {{\mathrm{d}}I_y} & = \frac{2 G M m}{v}\frac{1}{b^2} \times \left\{ \frac{b^2(b^2 - r_c^2)}{(b^2 + r_c^2)^2}, \frac{2r_c^4 b^2 - 3 r_c^2 b^4 - b^6}{(b^2 + r_c^2)^3} \right\} {\mathrm{d}b} \end{aligned} \]

それぞれのポテンシャルに依る潮汐効果の大きさと, 質点が作るポテンシャルに依る潮汐効果との比を図示しました. 潮汐効果はポテンシャルの中心付近で最大値をとります. 特徴的な半径 \(r \sim r_c\) よりも遠くではおおむね質点ポテンシャルによる潮汐効果に漸近します.

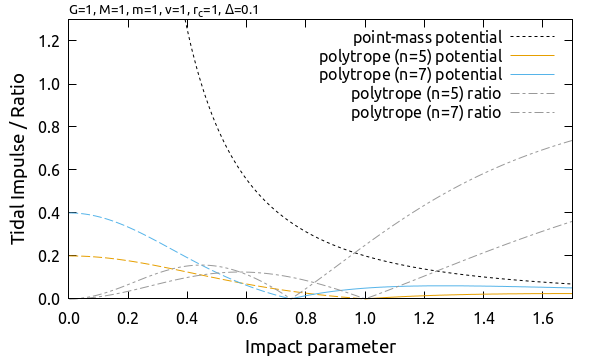
質点がつくるポテンシャル以外の 3 つのポテンシャルに依る潮汐効果の大きさを比較します. ただし \(R = r_c\) としました. いずれも球の内部では質点がつくるポテンシャルとは逆向き (\(\mathbf{b}\) の向きに押しつぶされる方向) に潮汐効果が発生する傾向があります.

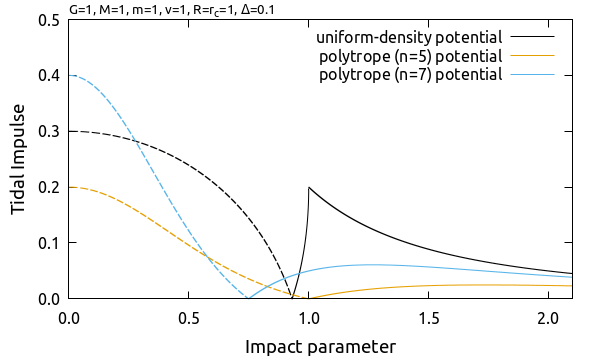
Comparison of tidal impulses for different potentials

潮汐効果の大きさはポテンシャルの中心付近 (\(b \simeq 0\)) で最大値をとり, 大きさは以下の順番になりました.

\[ |{\mathrm{d}}I_{y, \text{poly7}}| > |{\mathrm{d}}I_{y, \text{unif}}| > |{\mathrm{d}}I_{y, \text{poly5}}| \]

衝突パラメタがある距離よりも大きくなると, 潮汐効果は質点が作るポテンシャルに依る影響に漸近します. 一様密度のケースでは質点が作るポテンシャルに不連続に遷移するため, kink が出現しています. 現実には密度分布はなだらかに変化すると考えられるため, kink はいくぶんなまって丸められた形状になると考えられます.

受ける力の最大値は \(b^{-2}\) に比例しますが, 力が “ほぼ最大” になる経路の長さがだいたい \(b\) に比例するため, 依存性は結果的に \(b^{-1}\) となるようです. ↩
奇数のときは解析解がありそうな感じですが \(n\) が大きくなるとどんどん煩雑になりそうです. ↩

Last update: April 4, 2024