Variance of Variance
とある正規分布にしたがうデータを \(N\) 個取得することを考えます.
\[
x_i \sim \mathcal{N}(\mu, \sigma^2)
\]
ここで \(\mathcal{N}(\mu, \sigma^2)\) は平均が \(\mu\) で分散が \(\sigma^2\) の正規分布を表します. このとき \(N\) 個のデータ \(\{x_i\}\) から計算される統計量としてサンプル平均とサンプル分散があります.
\[
\begin{aligned}
\tilde{\mu} & = \frac{1}{N}\sum_{i=1}^{N} x_i \\
\tilde{\sigma}^2 & = \frac{1}{N-1}\sum_{i=1}^{N} (x_i - \tilde{\mu})^2
\end{aligned}
\]
このサンプル平均とサンプル分散は母集団のパラメタ \(\mu\), \(\sigma^2\) をどの程度よく再現しているかを考えます.
サンプル平均の分散
まずサンプル平均について確認します. サンプル平均の分散 \(V^2(\tilde{\mu})\) を計算してみましょう.
\[
V^2(\tilde{\mu})
= V^2\left( \frac{1}{N}\sum_{i=1}^{N} x_i \right)
= \frac{1}{N^2} \sum_{i=1}^{N} V^2\left( x_i \right)
= \frac{\sigma^2}{N}
\]
ここで \(x_i \sim \mathcal{N}(\mu, \sigma^2)\) であることと, それぞれのデータは独立であることを使用して式変形をしました. 「平均値の誤差 (分散) はサンプルの分散を \(N\) で割ったものである」というよく知られた関係が得られます.
サンプル分散の分散
それではサンプル分散の場合はどうでしょうか. 同様に分散を計算してみます.
\[
\begin{aligned}
V^2(\tilde{\sigma}^2)
& = V^2\left( \frac{1}{N-1}\sum_{i=1}^{N} (x_i - \tilde{\mu})^2 \right) \\
& = \frac{1}{(N-1)^2}
V^2\left( \sum_{i=1}^{N} \left[
(x_i - \mu)^2 -2(x_i - \mu)(\mu - \tilde{\mu}) + (\mu - \tilde{\mu})^2
\right]\right)
\end{aligned}
\]
最初の項は次のように計算できます.
\[
\begin{aligned}
V^2\left( \sum_{i=1}^N (x_i - \mu)^2 \right)
& = V^2\left( \sum_{i=1}^N \sigma^2 \left(\frac{x_i - \mu}{\sigma} \right)^2 \right) \\
& = \sigma^4 V^2\left( \sum_{i=1}^N z_i^2
\right) \\
& = 2 N \sigma^4
\end{aligned}
\]
ここで \(z_i = (x_i - \mu)/\sigma\) とおき, \(\chi^2 = \sum^N z_i\) は自由度 \(N\) の \(\chi^2\) 分布にしたがうこと, およびその分散が \(2N\) であることを使用しました. 次の項は \(\tilde{\mu}\) と \(x_i\) が独立ではないので計算が難しそうです. 正確ではありませんが \(x_i - \mu\) と \(\mu - \tilde{\mu}\) が無相関だと思って大きさを見積もってみます.
\[
\begin{aligned}
V^2\left( \sum_{i=1}^N (x_i - \mu)(\mu - \tilde{\mu}) \right)
& = \sum_{i=1}^N V^2\left( (x_i - \mu)(\mu - \tilde{\mu}) \right) \\
& = \sum_{i=1}^N \left[
E\left( \left[(x_i - \mu)(\mu - \tilde{\mu})\right]^2 \right) -
E\left( (x_i - \mu)(\mu - \tilde{\mu}) \right)^2
\right] \\
& = \sum_{i=1}^N \left[
E((x_i - \mu)^2) E((\mu - \tilde{\mu})^2) -
E((x_i - \mu))^2 E((\mu - \tilde{\mu}))^2
\right] \\
& = \sum_{i=1}^N \left[
\sigma^2 \cdot \frac{\sigma^2}{N} - 0 \cdot 0
\right] \\
& = \sigma^4
\end{aligned}
\]
ここでは \(V^2(X) = E(X^2) - E(X)^2\) (\(E(\cdot)\) は \(\cdot\) の平均値) という関係と \(X\), \(Y\) が無相関であるときに \(E(XY) = E(X)E(Y)\) であることを使用しました. この項の大きさは最初の項に比べてたかだか \(1/N\) 程度であることがわかります. 引き続いて最後の項を計算すると次のようになります.
\[
\begin{aligned}
V^2\left( \sum_{i=1}^N (\mu - \tilde{\mu})^2 \right)
& = N^2 V^2\left( (\mu - \tilde{\mu})^2 \right) \\
& = N^2 V^2\left( \frac{\sigma^2}{N}
\left(\frac{\mu - \tilde{\mu}}{\sigma/\sqrt{N}}\right)^2 \right) \\
& = \sigma^4 V^2\left( \zeta^2 \right) \\
& = 2\sigma^4
\end{aligned}
\]
ここでは最初の項と同様に \(\zeta^2\) が自由度 1 の \(\chi^2\) 分布にしたがうとして計算しました. この項も最初の項にくらべてたかだか \(1/N\) 程度の大きさしかないことがわかります.
それぞれを代入するとサンプル分散の分散を以下のように見積もることができます.
\[
\begin{aligned}
V^2(\tilde{\sigma}^2)
& = \frac{1}{(N-1)^2} \left[ 2N\sigma^4 -2\sigma^4 +2\sigma^4 \right] \\
& = \frac{2N}{(N-1)^2}\sigma^4
\end{aligned}
\]
標準偏差の分散
最後に標準偏差の分散について考えてみます. サンプルから推定した標準偏差 \(\tilde{\sigma}\) はサンプル分散の正の平方根として与えられます (\(\tilde{\sigma} = \sqrt{\tilde{\sigma}^2}\)). この定義から標準偏差の分散を計算してみます. ただし, ここでは簡略化のために分散の分散で計算した最初の項だけを取り扱うことにします.
\[
\begin{aligned}
V^2(\tilde{\sigma})
& = V^2\left( \sqrt {\frac{1}{N-1}\sum_{i=1}^{N} (x_i - \tilde{\mu})^2 } \right) \\
& = \frac{1}{N-1}
V^2\left( \sqrt{ \sum_{i=1}^{N} \left[
(x_i - \mu)^2 -2(x_i - \mu)(\mu - \tilde{\mu}) + (\mu - \tilde{\mu})^2
\right] } \right) \\
& \simeq \frac{1}{N-1}
V^2\left( \sqrt{ \sum_{i=1}^{N} (x_i - \mu)^2 } \right) \\
& = \frac{\sigma^2}{N-1}
V^2\left( \sqrt{ \sum_{i=1}^{N} \left(\frac{x_i - \mu}{\sigma}\right)^2 } \right) \\
& = \frac{\sigma^2}{N-1}
V^2\left( \sqrt{ \sum_{i=1}^{N} z^2 } \right)
\end{aligned}
\]
今度は \(V^2(\cdot)\) の中身は自由度が \(N\) の \(\chi\) 分布に従います. 自由度が \(k\) の \(\chi\) 分布の平均値 \(\mu\) と分散 \(\sigma^2\) は以下のとおりです. ここで \(\Gamma(\cdot)\) はガンマ関数です.
\[
\mu = \sqrt{2} \frac{\Gamma\left(\frac{k+1}{2}\right)}{\Gamma(\frac{k}{2})},
\quad
\sigma^2 = k - \mu^2
\]
\(k\) が十分に大きいとき \(\mu\) は \(\sqrt{k}\) に漸近します. もう少し正確に計算すると分散を以下の式で近似でき, \(k >> 1\) の領域では \(\chi\) 分布の分散は \(1/2\) に収束します.
\[
\sigma^2 = k - \mu^2
\simeq \frac{k}{2(k+1)}\left[ 1 + \mathcal{O}\left(\frac{1}{k}\right) \right]
\]
よって以下の式で標準偏差の分散を見積もることができます.
\[
\begin{aligned}
V^2(\tilde{\sigma})
& \simeq \frac{\sigma^2}{N-1}
V^2\left( \sqrt{ \sum_{i=1}^{N} z^2 } \right)
= \frac{\sigma^2}{2(N-1)}
\end{aligned}
\]
シミュレーションによる確認
乱数をもちいたシミュレーションによって結果をざっと確認してみます. サンプル数を \(N = 100\) として平均 \(\mu = 10\), 標準偏差 \(\sigma = 3.1\) にしたがう乱数を 1000 セット生成します. それぞれで統計量を計算して (累積) 確率分布を作成します. 上で計算した平均・分散を持つ正規分布の分布関数と比較します.
データは以下のように生成しました.
mu = 10
sigma = 3.1
N = 100
pkg load statistics
x = normrnd(mu, sigma, [N, 1e3]);
確率分布 (青実線) と期待される分布 (赤破線) をそれぞれプロットしました. いずれのケースでもシミュレーションで生成したサンプルの統計量分布をよく再現しています. \(N\) をより大きくすると差は縮まっていきます.
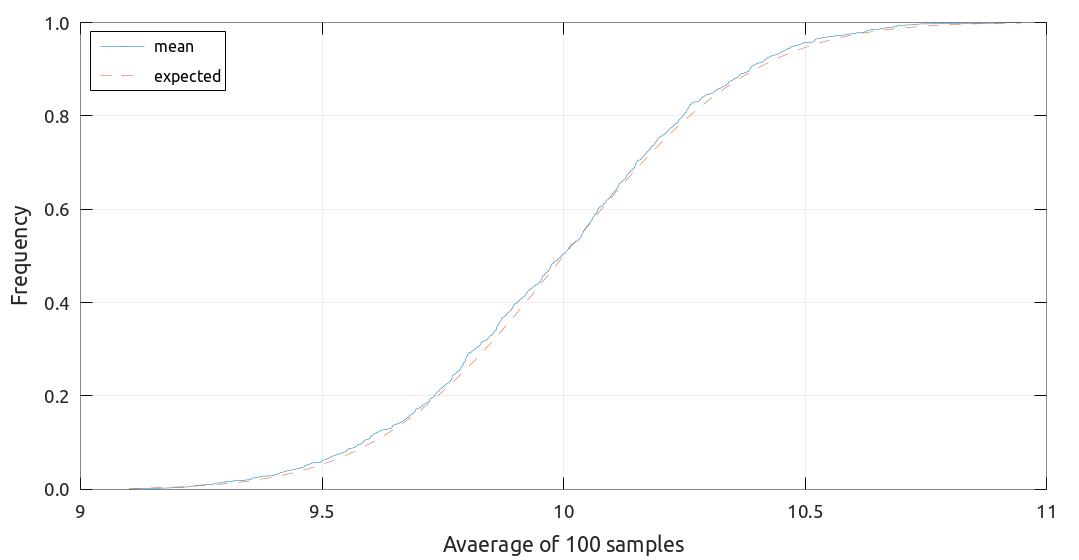平均について検証したケース
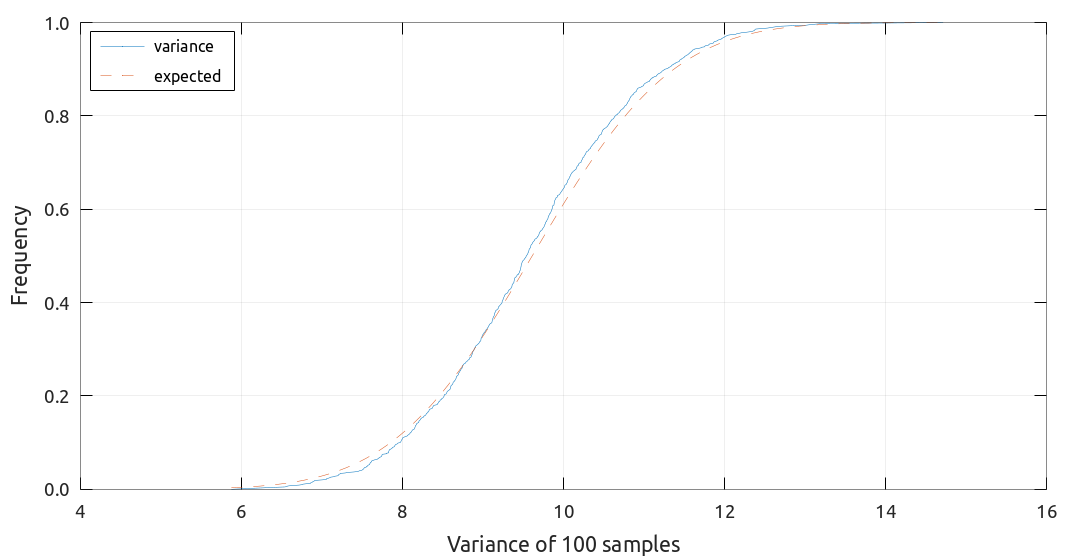分散について検証したケース
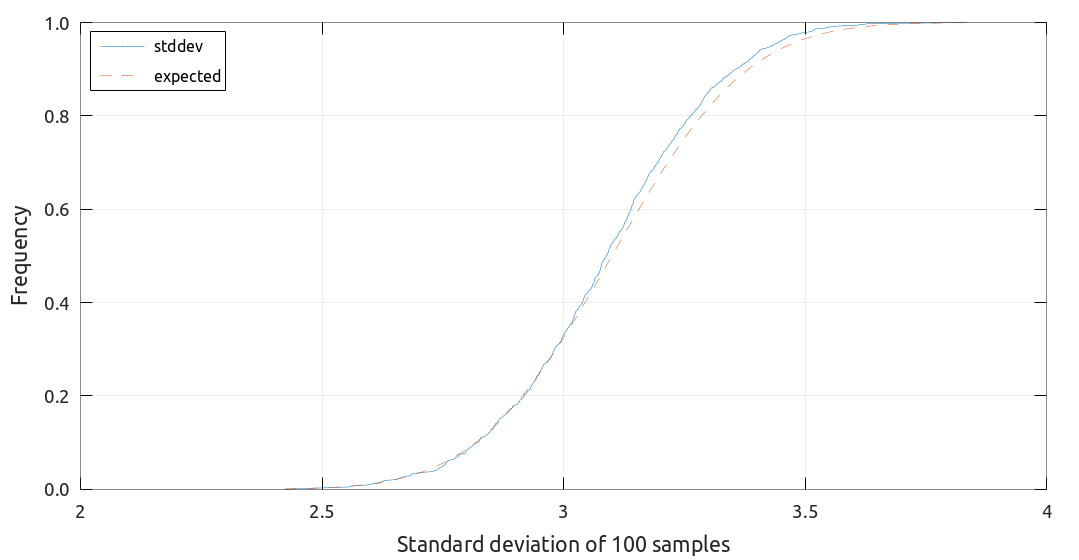標準偏差について検証したケース
参考文献