DCT 変換による fits ファイルの不可逆圧縮

観測装置の大規模化によって生産されるデータ量は増大しつつあります. しかし, 生み出されたデータのすべてがサイエンスに必要であるというわけではありません. 特にサーベイ観測においてはその傾向は顕著です. 天体密度が疎な領域では取得したデータの大部分は天体のいない空であり, 天体からの信号を反映しているピクセルはごく一部しかありません. リソースを有効活用するためには, データを非可逆的に圧縮することも検討する余地があります. ここでは JPEG 圧縮にも使われている離散コサイン変換をもちいて, 画像データを圧縮する方法について考察します.

離散コサイン変換

離散コサイン変換 (discrete cosine transformation, DCT) は等間隔でサンプルされた有限な信号列を偶関数になるような境界条件で展開してフーリエ変換したものに対応します. 定義は複数ありますが, 頻繁にもちいられる定義である DCT-II と DCT-III を以下に示します.

\[ \begin{aligned} \mbox{(DCT-II)}\quad & X_k = \sum^{N-1}_{i=0}x_k \cos\left[ \frac{\pi}{N}\left( n + \frac{1}{2} \right)k \right], \\ \mbox{(DCT-III)}\quad & X_k = \frac{1}{2}x_0 + \sum^{N-1}_{i=1}x_k \cos\left[ \frac{\pi}{N}n\left( k + \frac{1}{2} \right) \right]. \end{aligned} \]

DCT-II と DCT-III は互いに \(2/N\) 倍することで逆変換の関係になっています.

DCT による画像圧縮

JPEG 画像の圧縮は主に以下の手順で実行されます.

画像データを 8×8 pix のサブ領域 (\(I_{i,j}\)) に分割する,
サブ領域に 2 次元 DCT 変換を施す (\(I_{i,j} \rightarrow \mathcal{I}_{i,j}\)),
周波数成分をウェイトで割って整数化する (\(\mathcal{I}'_{i,j} = {\rm fix}\,\mathcal{I}_{i,j}/W_{i,j}\)),
周波数の低い順にデータを並び替える (\(\mathcal{I}'_{i,j} \rightarrow \mathcal{I}''_n\)),
ランレングス圧縮とハフマン符号化によってデータを圧縮する.

上記の過程のうち 3. が不可逆であるため, JPEG 形式で保存すると画像が劣化することになります. また, ウェイト係数 \(W_{i,j}\) の選び方によってこの劣化度合いをコントロールすることができます.

ここでは 1–4 までのプロセスを実行して画像データをバイナリ形式でファイルに保存します. データをそのまま保存したファイルと DCT 変換で情報を整理したファイルをそれぞれ gzip で圧縮して, 圧縮効率に差が生まれるかを調べることにします. SMOKA に保存されている KWFC のアーカイブから KWFC00432624.fits をダウンロードし, 1024×1024 のサブ領域を切り出したものをテストデータとして使用しました.

今回使用したウェイト係数を以下に記します.

W =

    128     64     64     32     32     32     32   8192
     64     16      8      8      8      8   2048   2048
     64      8      8      4      4   1024   1024   1024
     32      8      4      4    512   1024   1024   1024
     32      8      4    512    512   1024    512    512
     32      8   1024   1024   1024    512    512    512
     32   2048   1024   1024    512    512    512    512
   8192   2048   1024   1024    512    512    512    512

この係数は低周波数成分が 16 bit に, 高周波数成分が 8bit に収まるように適当に定めました. 変換のようすを以下の図に示します. 図 1 は変換前の画像であり, 図 2 は DCT 変換によって情報を落として劣化させたあとの画像です. ウェイト係数を適切に選択すれば, 目に見えてわかるような画質の劣化は確認できません.

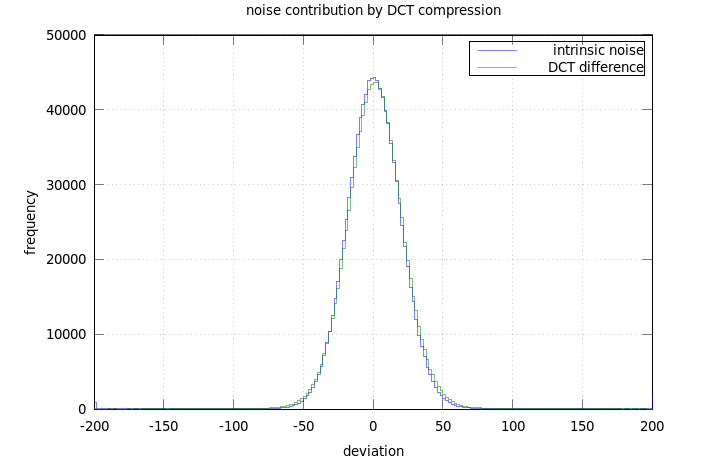
DCT 変換によってどれだけピクセルカウントが変化したのかを図 3 に示しました. オリジナル画像と DCT によって劣化した画像の差分をとり, ピクセル値のヒストグラムを緑実線で表示しました. 青実線はオリジナル画像のスカイ領域でのばらつきを表しています. DCT 変換によって高周波成分を落としたので, オリジナル画像と DCT 変換画像の差分はほとんどノイズ成分だと推測できます. ただし, サイエンスに影響がないかどうかは, 実際に天体を測光することでフラックスがどの程度保存されているのか確認する必要があります.

図 3. ピクセルカウントのヒストグラム. 青線はオリジナル画像のスカイ領域のばらつき. 緑線は DCT 変換による残差.

オリジナルのデータはすべてのピクセルが uint16 フォーマットで記述できます. 総ピクセル数は 1048576 (1024×1024) なのでファイルサイズは 2097152 byte になります. DCT 圧縮したデータは画像ではなく変換係数を保存します. 低周波数成分を 16 bit で高周波数成分を 8 bit で保存しました. 高周波数成分が 458752 (28×16384), 低周波数成分が 589824 (36×16384) だったのでファイルサイズは 1507328 byte になりました. なお, データを保存する際には周波数が低い順に並び替えて, 高周波数成分がデータの末尾に並ぶように整列させました.

データ圧縮結果

ls -l で調べたファイルサイズは以下の通りです. さきほど計算した通りにのファイルサイズなっています. このファイルを gzip で圧縮したところ, オリジナルデータ (origfits.dat) は 2097152 byte から 1241495 byte に圧縮されており, \(59\%\) の圧縮率となりました. DCT 変換後のデータ (reduced.dat) は 1507328 byte から 518115 byte に圧縮されており, \(34\%\) まで圧縮することができました.

## raw output data
-rw-rw-r-- 1 users users 2097152 Nov 18 18:15 origfits.dat
-rw-rw-r-- 1 users users 1507328 Nov 18 18:21 reduced.dat

## after gzip compression
-rw-rw-r-- 1 users users 1241495 Nov 18 18:15 origfits.dat.gz
-rw-rw-r-- 1 users users  518115 Nov 18 18:21 reduced.dat.gz

画像データをそのまま gzip で圧縮すると \(59\%\) 程度しか圧縮されないが, DCT 変換によって高周波成分を捨てることで圧縮率を 2 倍程度高めることができることがわかりました. サーベイ観測によって得られる画像に含まれる周波数成分にはあまり差はないだろうと考えられます. 適切なウェイト係数を求めることができれば, サイエンスに必要なデータを落とすことなく, データを効率よく圧縮できると期待されます.

今後の課題

今回はスカイ領域の統計的な性質と画像データの圧縮率だけを考察しました. 天体からのフラックスが保存されているかどうかは確認していません. 天体を測光したときの signal-to-noise ratio で議論することが必要です. また, 高周波成分はほとんどノイズだと考えられますが, この情報を落としてしまうことで観測時にどれだけのノイズが載っていたのかを後で見積もることができなくなってしまいます. データのクオリティを評価するために必要な情報をヘッダなどに残しておく必要があります. また, データ圧縮率とサイエンス両方に課せられる要求を満たすようなウェイト係数が存在するか, 存在するのであればどのように導出するのかは別途検討する必要があります.